Nested Dielectrics is a system that makes it easy to model complex transitions between two or more types of dielectrics. For example, the border of glass and water in a glass. If the glass boundary is complex, then duplicating this boundary for water can be difficult.
Suppose we need to model such a glass with water and air bubbles:
The ray goes from left to right and enters from the air into the glass at point 1. Then, at point 2, water begins. At point 3, the ray meets an air bubble, at point 4 it leaves it back into the water. At point 5 it exits the water into the glass and then at point 6 leaves the glass.
How can you organize the transition from one volumetric material to another?
Firstly, you can't just take two closed volumes and combine their borders - the triangles will be overlapped and this will lead to artifacts. The border should be modeled as a single triangle with double-sided material. Then the renderer can analyze these materials and assume that one dielectric is replaced by another. Normally renderers don't do this. Dali Renderer can do this, but this modeling option is not recommended, as there is a better way.
Secondly, the idea arises to take two closed volumes with different dielectrics and slightly space their boundary apart. This is absolutely wrong to do! The fact is that in physics there is the concept of "total internal reflection". If the angle between the beam and the surface is too small, then for the transition from one dielectric to another, a situation may arise in which the beam cannot cross the boundary at all, it is completely reflected back into the original dielectric. This angle depends on the ratio of the refractive indices of the first and second dielectric. If we spread the dielectrics over a negligibly small distance, then we introduce a third dielectric - vacuum (or air). In such a scheme, total internal reflection occurs at other angles, which eventually distorts the picture.
If we do not use the boundary, for which two dielectrics are explicitly defined, then there is only one way out - when passing through the scene, the ray must "remember" which dielectrics it has met and calculate the refractive index ratios for each intersection with a new material.
Nested Dielectrics is just such a mechanism. During ray tracing, a list of active materials is maintained. New materials enter it at the first intersection and are removed at the second. For this method to work, it is strictly necessary that the dielectric geometry be closed and belong to one model or one GeoID. You cannot split the sphere into two halves - in this case the second intersection will belong to another model and the material will not be removed from the list. If it is necessary to spread the dielectric over several materials or over several models (for example, different materials for the arms, legs and body of a character), within one logical model, then you can use the GeoID property, which is configured on the
Object Properties tab. Nested Dielectrics also adds the property of material to take precedence. This is the number set in the material GUI. The larger it is, the greater the priority of the material. If in some area of space there are materials with different priorities, then only those that have the highest priority will be considered. This allows for rough modeling in which the interface between dielectrics is not a single triangle or two-sided material. In this simulation, each dielectric is given with its own surface, but the volumes overlap slightly:
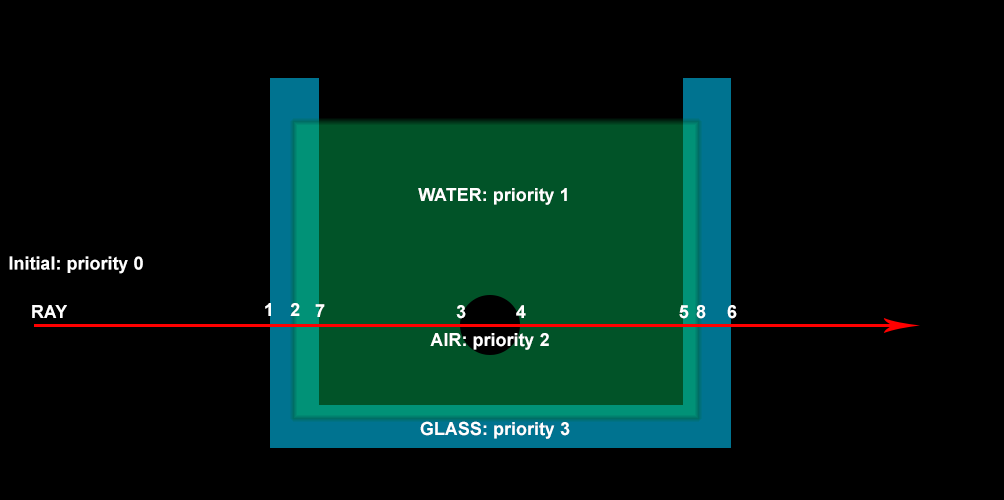
In the new scheme, the bounding surface for water penetrates the glass. At point 2 the beam encounters water, at a new point 7 removes glass from the list, at point 5 it encounters glass again, and at a new point 8 removes water from the list.
The priority of glass is higher than that of water and air - this means that wherever there is glass, this material will be used.
Air has priority over water. Thus, water will be everywhere where there is no glass and air bubbles.
Note that initially the beam does not have any assigned material, i.e. comes from a vacuum. If the camera is placed in a glass of water, then the initial values will be automatically calculated correctly.
Examples of working with priorities:
An example of subtracting volume with air from a dielectric:
And finally, a more complex picture. Both glasses have the same geometry and the second glass is an instance of the first, but additionally cut off by the volume with air: